Define and solve user equation

Basic example that show how to define the poisson equation and how to solve it with Dirichlet boundary conditions.

import fedoo as fd

Define a modeling space and add a variable “U” to this space A “2D” problem include by default the coordinates “X” and “Y”.

space = fd.ModelingSpace("2D")
U = space.new_variable("U")

Set the equation to solve on a weak form.

The space.derivative or space.variable functions create a differatial equation that we can combine with the +, - and * operators to build the weak form. the virtual properties set the variable as virtuals (in the sense of weak equations)

dU_dX = space.derivative("U", "X")
dU_dY = space.derivative("U", "Y")

wf = fd.WeakForm(dU_dX.virtual * dU_dX + dU_dY.virtual * dU_dY, name="Poisson Equation")

Define the integration domain (mesh)

mesh = fd.mesh.rectangle_mesh()

Assembly the global matrix, define a linear problem, add boundary conditions and solve the problem

fd.Assembly.create(wf, mesh, name="assembly")

pb = fd.problem.Linear("assembly")
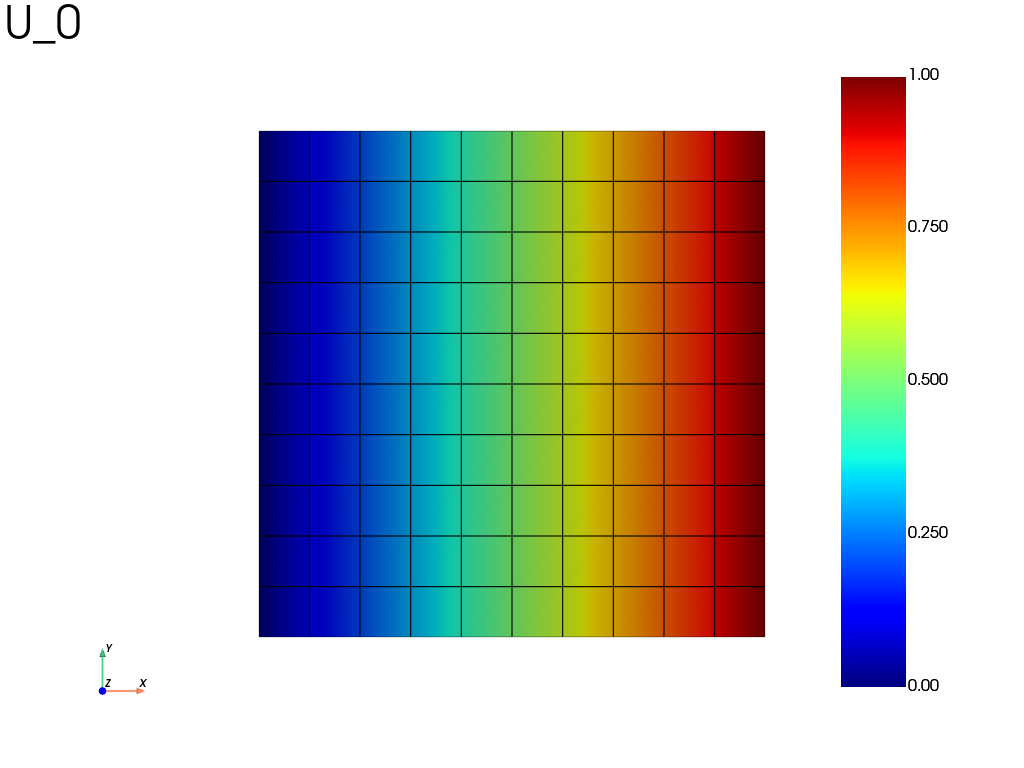
pb.bc.add("Dirichlet", "left", "U", 0)
pb.bc.add("Dirichlet", "right", "U", 1)

pb.solve()

res = pb.get_results("assembly", ["U"])
res.plot("U")