2D periodic boundary condition

Periodic boundary conditions are enforced on a 2D geometry with plane stress assumption (plate with hole). A mean strain tensor is enforced, and the resulting mean stress is estimated.

import fedoo as fd
import numpy as np

Dimension of the problem

fd.ModelingSpace("2Dstress")

<fedoo.core.modelingspace.ModelingSpace object at 0x7f61834fb370>

Definition of the Geometry

mesh = fd.mesh.hole_plate_mesh()

# alternative mesh below (uncomment the line)
# mesh = fd.mesh.rectangle_mesh(nx=51, ny=51)

Now define the problem to solve

# ------------------------------------------------------------------------------
# Material definition
# ------------------------------------------------------------------------------
fd.constitutivelaw.ElasticIsotrop(1e5, 0.3, name="ElasticLaw")

# ------------------------------------------------------------------------------
# Mechanical weak formulation
# ------------------------------------------------------------------------------
wf = fd.weakform.StressEquilibrium("ElasticLaw")

# ------------------------------------------------------------------------------
# Global Matrix assembly
# ------------------------------------------------------------------------------
fd.Assembly.create(wf, mesh, name="Assembly")

# ------------------------------------------------------------------------------
# Static problem based on the just defined assembly
# ------------------------------------------------------------------------------
pb = fd.problem.Linear("Assembly")

Add periodic constraint

Add a periodic conditions (ie a multipoint constraint) Some global dof are automatically added to the problem:

• ‘E_xx’, ‘E_yy’, ‘E_xy’ that refere to the mean strain components

• The global vector ‘MeanStrain’ is also added

pb.bc.add(fd.constraint.PeriodicBC(periodicity_type="small_strain"))

2D Periodic Boundary Condition:
name = 'Periodicity'

Add standard boundary conditions

# ------------------------------------------------------------------------------
# Macroscopic strain components to enforce
Exx = 0
Eyy = 0
Exy = 0.1

# Mean strain: Dirichlet (strain) or Neumann (associated mean stress) can be enforced
pb.bc.add("Dirichlet", "E_xx", Exx)  # EpsXX
pb.bc.add("Dirichlet", "E_xy", Exy)  # EpsXY
pb.bc.add("Dirichlet", "E_yy", Eyy)  # EpsYY

# Block one node to avoid singularity
center = mesh.nearest_node(mesh.bounding_box.center)
pb.bc.add("Dirichlet", center, "Disp", 0)

List of boundary conditions:
number of bc = 2

0: Dirichlet -> 'DispX' for 1 nodes set to 0
1: Dirichlet -> 'DispY' for 1 nodes set to 0

Solve and plot stress field

pb.solve()

# ------------------------------------------------------------------------------
# Post-treatment
# ------------------------------------------------------------------------------
res = pb.get_results("Assembly", ["Disp", "Stress", "MeanStrain"])

# plot the deformed mesh with the shear stress (component=3).
res.plot("Stress", "XY", "Node")

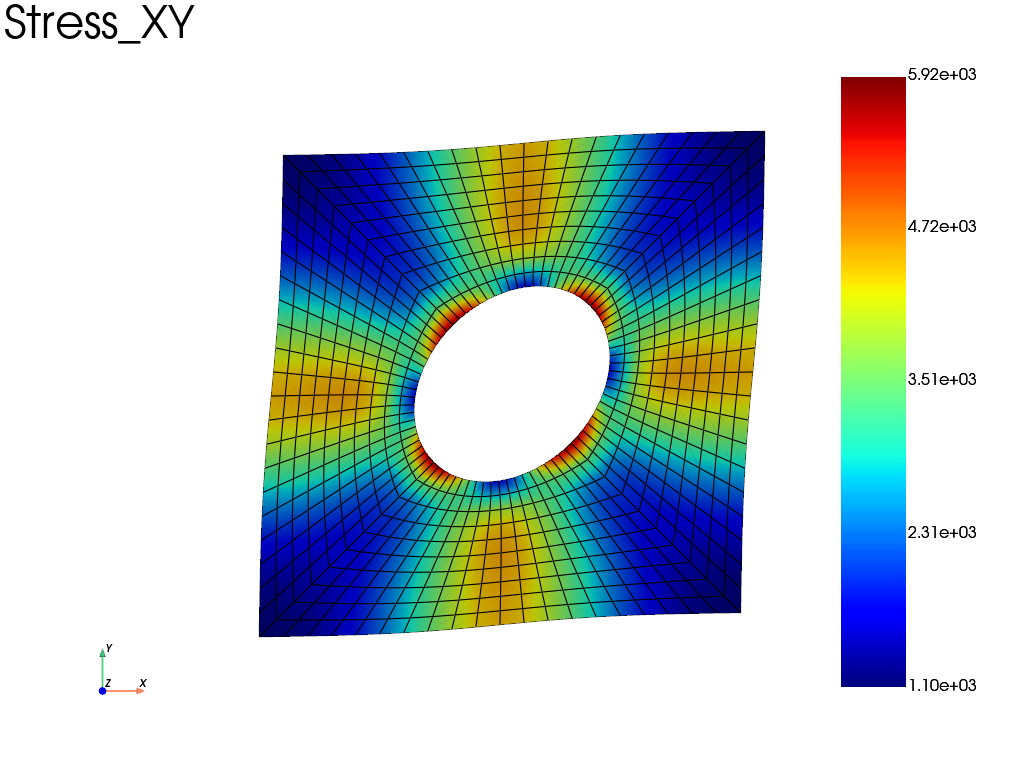
print the macroscopic strain tensor and stress tensor

print(
    "Strain tensor ([Exx, Eyy, Exy]): ",
    [pb.get_dof_solution(component)[0] for component in ["E_xx", "E_yy", "E_xy"]],
)

# Compute the mean stress tensor
surf = mesh.bounding_box.volume  # total surface of the domain = volume in 2d
mean_stress = [1 / surf * mesh.integrate_field(res["Stress"][i]) for i in [0, 1, 3]]

print("Stress tensor ([Sxx, Syy, Sxy]): ", mean_stress)

Strain tensor ([Exx, Eyy, Exy]):  [np.float64(0.0), np.float64(0.0), np.float64(0.1)]
Stress tensor ([Sxx, Syy, Sxy]):  [np.float64(-4.118837182431889e-12), np.float64(-9.570732117936132e-12), np.float64(2497.6680151186065)]