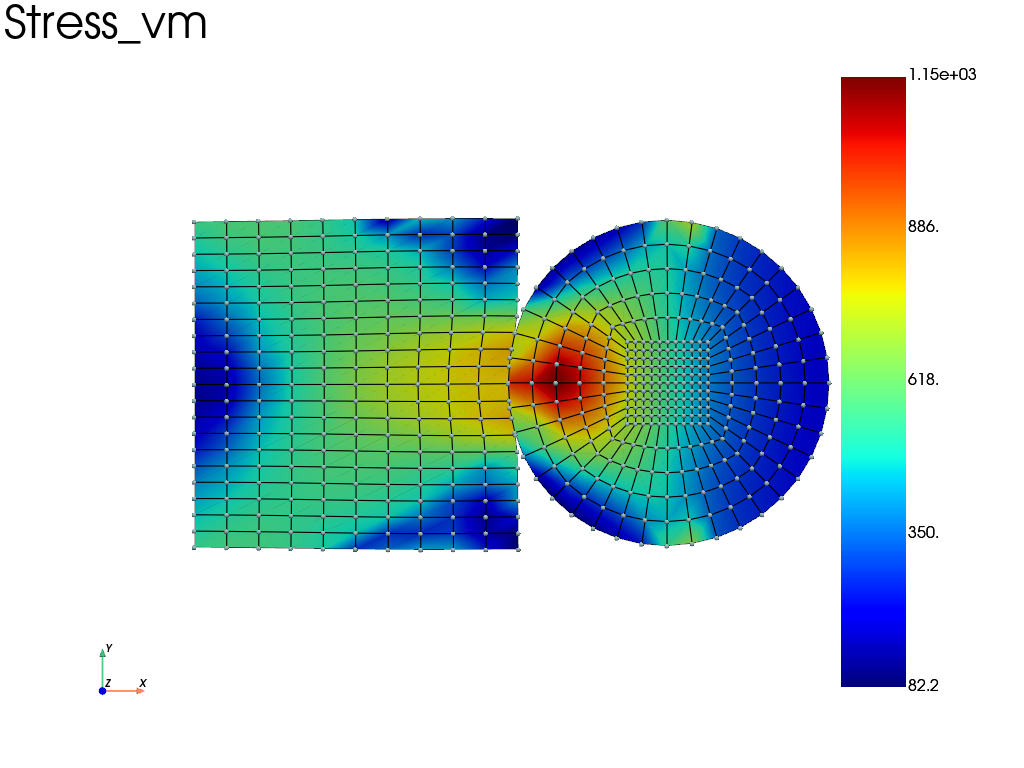
Contact bewteen a disk and a rectangle

Iter 1 - Time: 0.05000 - dt 0.05000 - NR iter: 2 - Err: 0.00326
Iter 2 - Time: 0.10000 - dt 0.05000 - NR iter: 1 - Err: 0.00154
Iter 3 - Time: 0.16250 - dt 0.06250 - NR iter: 1 - Err: 0.00446
Iter 4 - Time: 0.20000 - dt 0.07812 - NR iter: 1 - Err: 0.00357
Iter 5 - Time: 0.27813 - dt 0.07812 - NR iter: 3 - Err: 0.00086
Iter 6 - Time: 0.30000 - dt 0.07812 - NR iter: 0 - Err: 0.00387
Iter 7 - Time: 0.37813 - dt 0.07812 - NR iter: 2 - Err: 0.00126
Iter 8 - Time: 0.40000 - dt 0.07812 - NR iter: 0 - Err: 0.00288
Iter 9 - Time: 0.47813 - dt 0.07812 - NR iter: 2 - Err: 0.00069
Iter 10 - Time: 0.50000 - dt 0.07812 - NR iter: 0 - Err: 0.00228
Iter 11 - Time: 0.57812 - dt 0.07812 - NR iter: 1 - Err: 0.00469
Iter 12 - Time: 0.60000 - dt 0.09766 - NR iter: 0 - Err: 0.00190
Iter 13 - Time: 0.69766 - dt 0.09766 - NR iter: 2 - Err: 0.00068
Iter 14 - Time: 0.70000 - dt 0.09766 - NR iter: 0 - Err: 0.00017
Iter 15 - Time: 0.79766 - dt 0.09766 - NR iter: 1 - Err: 0.00418
Iter 16 - Time: 0.80000 - dt 0.12207 - NR iter: 0 - Err: 0.00019
Iter 17 - Time: 0.90000 - dt 0.12207 - NR iter: 1 - Err: 0.00413
Iter 18 - Time: 1.00000 - dt 0.12207 - NR iter: 1 - Err: 0.00391
Iter 19 - Time: 0.05000 - dt 0.05000 - NR iter: 0 - Err: 0.00264
Iter 20 - Time: 0.10000 - dt 0.06250 - NR iter: 0 - Err: 0.00278
Iter 21 - Time: 0.16250 - dt 0.06250 - NR iter: 0 - Err: 0.00368
Iter 22 - Time: 0.20000 - dt 0.07812 - NR iter: 0 - Err: 0.00231
Iter 23 - Time: 0.27813 - dt 0.07812 - NR iter: 1 - Err: 0.00047
Iter 24 - Time: 0.30000 - dt 0.09766 - NR iter: 0 - Err: 0.00152
Iter 25 - Time: 0.39766 - dt 0.09766 - NR iter: 1 - Err: 0.00127
Iter 26 - Time: 0.40000 - dt 0.12207 - NR iter: 0 - Err: 0.00059
Iter 27 - Time: 0.50000 - dt 0.12207 - NR iter: 2 - Err: 0.00207
Iter 28 - Time: 0.60000 - dt 0.12207 - NR iter: 1 - Err: 0.00000
Iter 29 - Time: 0.70000 - dt 0.12207 - NR iter: 1 - Err: 0.00000
Iter 30 - Time: 0.80000 - dt 0.12207 - NR iter: 1 - Err: 0.00000
Iter 31 - Time: 0.90000 - dt 0.12207 - NR iter: 1 - Err: 0.00000
Iter 32 - Time: 1.00000 - dt 0.12207 - NR iter: 1 - Err: 0.00000

import fedoo as fd
import numpy as np


fd.ModelingSpace("2D")

NLGEOM = "UL"  # updated lagrangian

# parameters
h = 1
L = 1
E = 200e3
nu = 0.3
alpha = 1e-5

# mesh of the rectangle
mesh_rect = fd.mesh.rectangle_mesh(
    nx=11, ny=21, x_min=0, x_max=L, y_min=0, y_max=h, elm_type="quad4", name="Domain"
)
mesh_rect.element_sets["rect"] = np.arange(0, mesh_rect.n_elements)

# mesh of a disk
mesh_disk = fd.mesh.disk_mesh(radius=L / 2, nr=6, nt=6, elm_type="quad4")
mesh_disk.nodes += np.array([1.5, 0.48])  # translate the disk
mesh_disk.element_sets["disk"] = np.arange(0, mesh_disk.n_elements)

# put the two meshes in a sigle meshes (change the element indices)
mesh = fd.Mesh.stack(mesh_rect, mesh_disk)

# node sets for boundary conditions
nodes_left = mesh.find_nodes("X", 0)
nodes_right = mesh.find_nodes("X", L)

nodes_bc = mesh.find_nodes("X>1.5")
nodes_bc = list(set(nodes_bc).intersection(mesh.node_sets["boundary"]))

# if slave surface == disk
# nodes_contact = mesh.node_sets['boundary']
# surf = fd.mesh.extract_surface(mesh.extract_elements('rect')) #extract the surface of the rectangle
# surf = surf.extract_elements(surf.get_elements_from_nodes(nodes_right))

# if slave surface == rectangle
nodes_contact = nodes_right
surf = fd.mesh.extract_surface(
    mesh.extract_elements("disk")
)  # extract the surface of the disk

# define contact assembly
contact = fd.constraint.Contact(nodes_contact, surf)

# change contact parameters
contact.contact_search_once = True  # search contact only once per time increment
contact.eps_n = 5e5  # contact rigidity
contact.max_dist = 1  # ignore contact if dist > 1

# define material for rectangle (elasto-plastic law)
Re = 300
k = 1000  # 1500
m = 0.3  # 0.25
props = np.array([E, nu, alpha, Re, k, m])
material_rect = fd.constitutivelaw.Simcoon("EPICP", props, name="ConstitutiveLaw")

# define material for disk (elastic isotropic)
material_disk = fd.constitutivelaw.ElasticIsotrop(50e3, nu, name="ConstitutiveLaw")

# define an heterogeneous constitutive law
material = fd.constitutivelaw.Heterogeneous(
    (material_rect, material_disk), ("rect", "disk")
)

# stress equilibrium weak form and related assembly
wf = fd.weakform.StressEquilibrium(material, nlgeom=NLGEOM)
solid_assembly = fd.Assembly.create(wf, mesh)

# add contact to the global assembly
assembly = fd.Assembly.sum(solid_assembly, contact)

# definie non linear analysis
pb = fd.problem.NonLinear(assembly)

# add some output that are automatically saved
results = pb.add_output(
    "contact_example", solid_assembly, ["Disp", "Stress", "Strain", "Statev", "Fext"]
)

# boundary conditions
pb.bc.add("Dirichlet", nodes_left, "Disp", 0)
pb.bc.add("Dirichlet", nodes_bc, "Disp", [-0.05, 0.025])

# set newton-raphson convergence criterion
pb.set_nr_criterion("Displacement", err0=None, tol=5e-3, max_subiter=5)

# solve load step
pb.nlsolve(dt=0.05, tmax=1, update_dt=True, print_info=1, interval_output=0.1)
n_iter_load = results.n_iter

# change boundary condition (unload)
pb.bc.remove(-1)  # remove last boundary contidion
pb.bc.add("Dirichlet", nodes_bc, "Disp", [0, 0])

# solve unload step
pb.nlsolve(dt=0.05, tmax=1, update_dt=True, print_info=1, interval_output=0.1)

# =============================================================
# Example of plots with pyvista - uncomment the desired plot
# =============================================================

# ------------------------------------
# Simple plot with default options
# ------------------------------------
results.load(n_iter_load - 1)  # load state at the end of load
results.plot("Stress", "vm", "Node", show=True, scale=1, show_nodes=True)

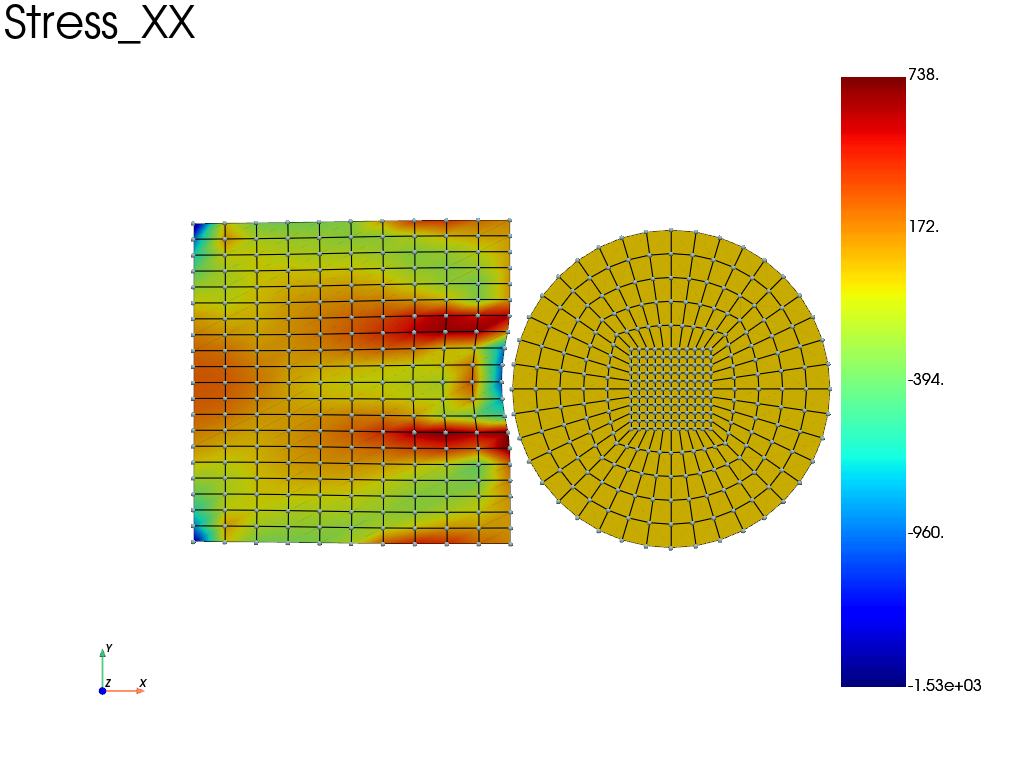
results.load(-1)  # load state at the end of load
results.plot("Stress", "XX", "Node", show=True, scale=1, show_nodes=True)
# results.plot('Fext',  'X', 'Node', show = True, scale = 1, show_nodes=True)

# results.plot('Disp', 0, 'Node', show = True, scale = 1, show_nodes=True)

# ------------------------------------
# Write movie with default options
# ------------------------------------
# results.write_movie(res_dir+filename, 'Stress', 'vm', framerate = 5, quality = 5)
# results.write_movie(res_dir+filename, 'Stress', 'XX', 'Node', framerate = 24, quality = 5, clim = [-3e3, 3e3])

# ------------------------------------
# Save pdf plot
# ------------------------------------
# pl = results.plot('Stress', 'vm', show = False)
# pl.save_graphic('test.pdf', title='PyVista Export', raster=True, painter=True)

# ------------------------------------
# Plot time history
# ------------------------------------
# from matplotlib import pylab
# t, sigma = results.get_history(('Time','Stress'), (0,12), component = 3)
# pylab.plot(t,sigma)
# #or results.plot_history('Stress', 12)