Canteleaver Beam using 3D hexahedral elements

import fedoo as fd

Pre-treatment: Mesh and problem definition

# Units: N, mm, MPa
mesh = fd.mesh.box_mesh(
    nx=51,
    ny=7,
    nz=7,
    x_min=0,
    x_max=1000,
    y_min=0,
    y_max=100,
    z_min=0,
    z_max=100,
    elm_type="hex8",
    name="Domain",
)

fd.ModelingSpace("3D")

# Material definition
fd.constitutivelaw.ElasticIsotrop(200e3, 0.3, name="ElasticLaw")
wf = fd.weakform.StressEquilibrium("ElasticLaw")

# Assembly
assembly = fd.Assembly.create(wf, mesh, "hex8")

# Type of problem
pb = fd.problem.Linear(assembly)

# Boundary conditions
nodes_left = mesh.node_sets["left"]
nodes_right = mesh.node_sets["right"]
nodes_top = mesh.node_sets["top"]
nodes_bottom = mesh.node_sets["bottom"]

pb.bc.add("Dirichlet", nodes_left, "Disp", 0)
pb.bc.add("Dirichlet", nodes_right, "DispY", -50)

Dirichlet boundary condition:
var = 'DispY'
n_nodes = 49
value = -50

Solver: use conjugate gradient method

# pb.set_solver('cg') #uncomment for conjugate gradient solver
pb.solve()

Post-treatment: Get and plot results

# Get the displacement vector
U = pb.get_disp()

# Get the stress and strain tensor at nodes
res = pb.get_results(assembly, ["Stress", "Strain", "Disp"], "Node")
stress = res["Stress"]
strain = res["Strain"]

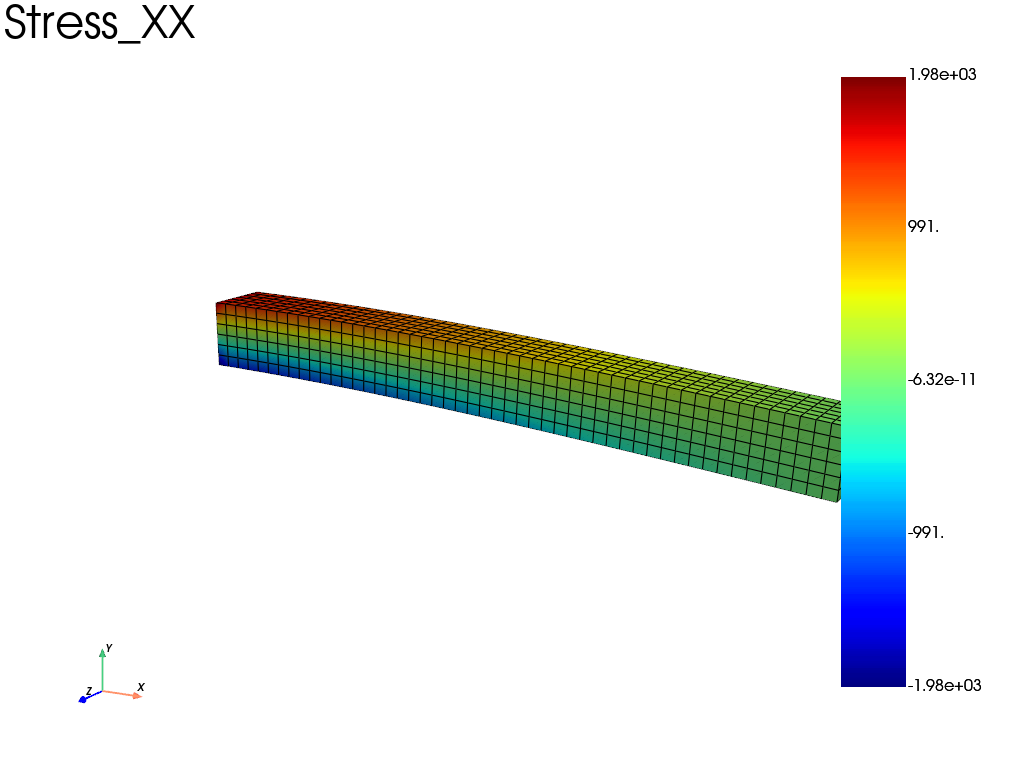
# plot the stress (xx component)
res.plot("Stress", "XX")