Compression of a ping pong ball

Example that show how to use plate elements with a pressure load.

import fedoo as fd
import pyvista as pv
import numpy as np

The problems parameters

E = 2e3  # MPa
nu = 0.37
radius = 20  # mm
thickness = 0.45  # mm
pressure = 10  # MPa

Create a simple sphere mesh using pyvista.

mesh = fd.Mesh.from_pyvista(pv.Sphere(radius))

Define a linear isotropic material and an homogeneous shell section

material = fd.constitutivelaw.ElasticIsotrop(E, nu, name="Material")
shell_section = fd.constitutivelaw.ShellHomogeneous("Material", thickness)

Define the weakform and associated assembly for plate model For plate elements, we first need to create a 3D modeling space

fd.ModelingSpace("3D")
wf = fd.weakform.PlateEquilibrium(shell_section)
solid_assembly = fd.Assembly.create(wf, mesh)

Select mesh elements where we will apply the pressure. The mesh.find_elements method is used with an arbitrary exression. Here we select all elements whose z coordinates are less that 3mm from minimal or maximal z value (sphere extremity along the z axis.

boundaries = mesh.find_elements(
    f"Z>{mesh.bounding_box.zmax-3} or Z<{mesh.bounding_box.zmin+3}"
)

Now we build the pressure assembly by extracting the surface mesh. The pressure assembly is then added to the solid_assembly to form the global assembly.

pressure_assembly = fd.constraint.Pressure(
    mesh.extract_elements(boundaries),
    pressure,
)
assembly = solid_assembly + pressure_assembly

Define a linear analysis and solve the problem.

Note

Here we don’t need to add other boundary conditions. The rigid body displacements and rotations of the sphere aren’t constrained but the solver find a solution that is unique in terms of strain and stress (but not for displacements or rotations)

pb = fd.problem.Linear(assembly)
pb.solve()

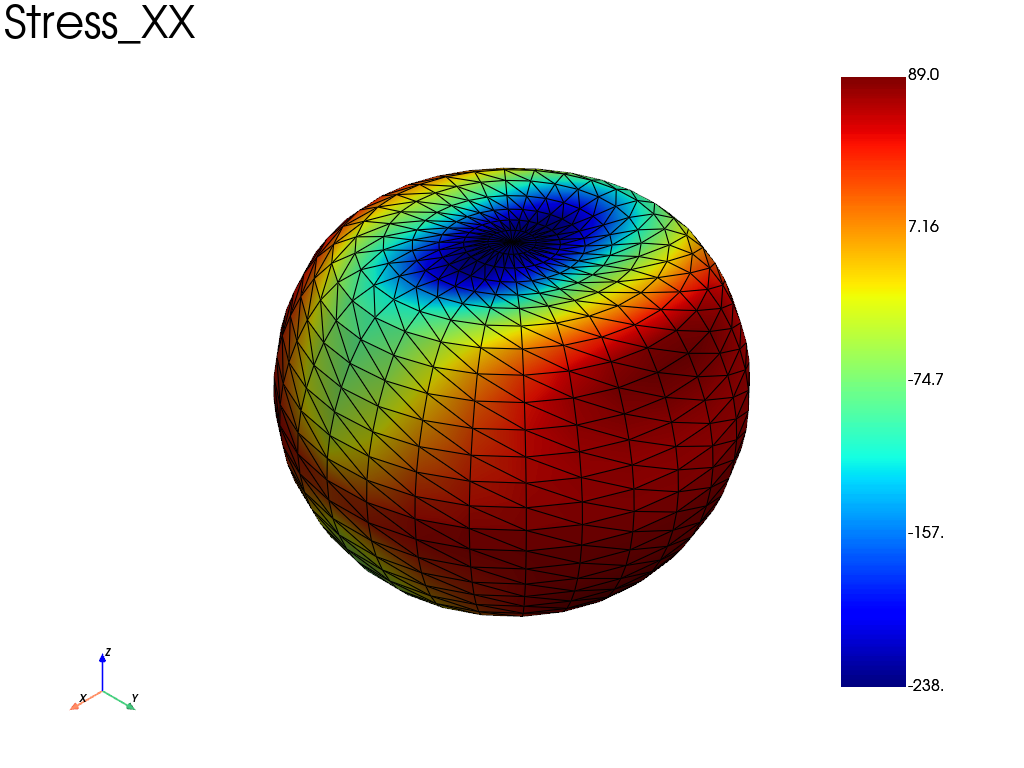
Extract the results: position = 1 is set for the surface along the positif direction of the normal vector (0 is the mean plane). The strains and stresses components are defined in the element local coordinate system (mesh.get_element_local_frame()).

res = pb.get_results(solid_assembly, ["Disp", "Rot", "Stress", "Strain"], position=1)
pl = pv.Plotter()
res.plot("Stress", component="XX", data_type="Node", plotter=pl)
pl.view_isometric()
pl.show()