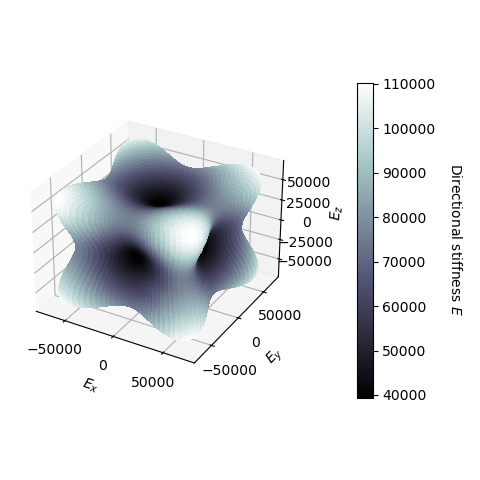
Effective properties of a cubic material

This tutorial studies the directional stiffness of a cubic material

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm, colors
from simcoon import simmit as sim
import os

Define a grid of directions in 3D space using spherical coordinates (θ, φ) and compute the components of the unit vector n.

phi = np.linspace(0, 2 * np.pi, 128)  # azimuthal angle in the xy-plane
theta = np.linspace(0, np.pi, 128).reshape(128, 1)  # polar angle

n_1 = np.sin(theta) * np.cos(phi)
n_2 = np.sin(theta) * np.sin(phi)
n_3 = np.cos(theta) * np.ones(128)

n = (
    np.array([n_1 * n_1, n_2 * n_2, n_3 * n_3, n_1 * n_2, n_1 * n_3, n_2 * n_3])
    .transpose(1, 2, 0)
    .reshape(128, 128, 1, 6)
)

Use Simcoon to obtain the cubic stiffness matrix L and its inverse (compliance M).

C11 = 185000.0
C12 = 158000.0
C44 = 39700.0

L = sim.L_cubic([C11, C12, C44], "Cii")
M = np.linalg.inv(L)

Compute the directional stiffness E(n) = 1 / (nᵀ·M·n) for all directions.

S = (n @ M @ n.reshape(128, 128, 6, 1)).reshape(128, 128)
E = 1.0 / S

x = E * n_1
y = E * n_2
z = E * n_3

Plot the directional stiffness as a 3D surface.

fig = plt.figure(figsize=plt.figaspect(1))
ax = fig.add_subplot(111, projection="3d")

norm = colors.Normalize(vmin=np.min(E), vmax=np.max(E), clip=False)
surf = ax.plot_surface(
    x,
    y,
    z,
    rstride=1,
    cstride=1,
    norm=norm,
    facecolors=cm.bone(norm(E)),
    linewidth=0,
    antialiased=False,
    shade=False,
)

ax.set_xlabel(r"$E_x$")
ax.set_ylabel(r"$E_y$")
ax.set_zlabel(r"$E_z$")

scalarmap = cm.ScalarMappable(cmap=plt.cm.bone, norm=norm)
cbar = fig.colorbar(scalarmap, ax=ax, shrink=0.7, pad=0.15)
cbar.set_label(r"Directional stiffness $E$", rotation=270, labelpad=20)

plt.tight_layout()
plt.show()